$M=0$なら巡回置換に分解して数える典型問題。また、$N=5$程度なら各順列を頂点として0-1BFSで探索すればよい。
満点について。まず、2つのロボットが与えられたときに、「少なくともいっぽうのインデックスが等しい」という関係が同値関係になっていることに注目する。このため、$N$個のインデックスはノーコストで自由に行き来できるまとまりに分割できる。
具体例を挙げて考える:
1
9 5
5 8 2 4 6 7 9 3 1
2 5
5 6
3 4
7 8
8 9
この入力をグラフで図示すると次のような感じになる:

各頂点は、コスト0で相互に行き来できるインデックスを1つにまとめたものである。また、辺$A \rightarrow B$は$A$に含まれる場所から$B$に含まれる場所にちょうど1つの数を移動させなければならないことを表す。たとえば$5$は最初インデックス$1$にあって、インデックス$5$に移動させたいので、頂点$1$から頂点$5(, 2, 6)$に辺を張っている。
こうしてグラフにしてみると、$M=0$の場合と考え方はあまり変わらないことに気づく。つまり、このグラフ上の長さ$k$の閉路は$k-1$回のスワップで解消できるので、グラフをいくつかの(辺素な)閉路に分割する問題であることがわかる。また、必要なスワップの回数は閉路の総数のみによって決まることも変わらない。
さて、閉路の総数だが、下のグラフのように分割方法によって異なる場合がある。
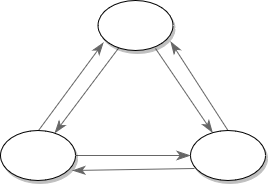
このグラフでは、長さ2の閉路を3つ選ぶことも長さ3の閉路を2つ選ぶこともできる。したがって、スワップの回数を減らすために、できるだけ多くの閉路に分割する方法を考えなければならない。ここまで考察を進めるとbitDPの形が見えた:
$\operatorname{dp}[S][x][y] :=$ 辺の集合$S$を使用済みで、いま作りかけている閉路(まだ閉じていない)の始点が$x$、終点が$y$である時の、今までに作った閉路の総数の最大値。
遷移が${O}(N)$なので計算量は${O}(N^32^N)$になる。オーダー的には微妙なところだが、大半の状態は無効だし、各$N$がすべて$18$ということもありえないので大丈夫だろう。割と余裕で通った。(計算量の評価がtightじゃないかも) 辺数が${O}(N)$だから隣接リストで持てば${O}(N^2 2^N)$だった。