2020年5月28日木曜日
JOI2010 春合宿 - Sengoku
$(i, j)$を通る傾き$1$の直線の切片は$j-i$で、傾き$-1$の直線の切片は$i+j$になる。
とりあえず重複のことは忘れて番兵毎に数えると、傾き$1$の直線の通るマスは$L - |i-j|$個あり、傾き$-1$の直線の通るマスは$i+j < L$のとき$i+j+1$個、$i+j \ge L$のとき$2L - (i+j+1)$個あることがわかるので、まずはこれらの総和が基本になる。
次に、重複を除くことを考える。まず、切片と傾きが同じ直線は完全に重なるので、登場した切片を記録しておいて、前に見たものは無視することで重複を避けられる。
最後に傾き$1$の直線と傾き$-1$の直線の交点の数を引く必要がある。まず、交点が格子点になるのは切片が偶数同士、奇数同士の場合なので、切片が偶数の直線についてのみ考えることにする。(奇数のものの交点も同様に数えられる。) 傾き$1$で切片が$C$の直線と傾き$-1$の直線が与えられた領域内で交わるのは、後者の切片が$[|C|, 2(L-1) - |C|$]に入っているとき、またその時に限るので、ソートしておいてそれぞれ二分探索で数えられる。
2020年5月25日月曜日
CodeChef May Cook-Off - Chefina on a Trip
無向辺を2つの有向辺と見て、スコアが下がる向きに重み$-1$、上がる向きに$+1$、変わらないなら$0$を付与すると、ある有向パスが上りになっている$\Leftrightarrow \min$クエリが$1$である、下りになっている$\Leftrightarrow \max$クエリが$-1$である、と判定できる。
ダブリングLCAの構築をする時に、同時にmin/maxについてもダブリングのテーブルを作っておけばパス$u - v$がbeautifulかどうかは適当に判定できる:
- $u$から根に向けてスコアが上がる限りダブリングで上る。$\operatorname{LCA}(u, v)$の深さより上(inclusive)に行けたら3に行く。
- さらに根に向けてスコアが下がる限り上る。$\operatorname{LCA}(u, v)$の深さより上に行けなかったらfalseを返す。$\operatorname{LCA}(u, v)$の深さより上に行けたら頂上が$u- \operatorname{LCA}$の側にあると記録しておく。
- $v$から根に向けてスコアが上がる限り上る。$\operatorname{LCA}(u, v)$の深さより上に行けたらtrueを返す。頂上が$u-\operatorname{LCA}$の側にあるのに$\operatorname{LCA}(u, v)$の深さより上に行けなかったらfalse。
- さらに根に向けてスコアが下がる限り上る。$\operatorname{LCA}(u, v)$の深さより上に行けたらtrueを返す。
- falseを返す。
山のイメージに従って書くだけなので特に難しいとは感じなかった。でも、振り返ってみると、$u$と$v$を完全に対称に扱ったほうがいい気がする。
2020年5月24日日曜日
パ研コンペティション3日目 E - 美しい和音
$f(i, x) := A_1, ..., A_i$を使って作れる総和$x$の美しい和音の総数、とする。$f$の漸化式は$A_i$を使う/使わないの二択の和で$f(i, x) = f(i-1, x) + f(i-2, x-A_i)$と書ける。これでDPすれば部分点が取れる。
また、DPのほとんどの枝で不可能な状態の遷移をしていることに注目すると高速化できる。例えば、$A_1, ..., A_i$から作れる美しい和音の最大スコア$g(i)$がDPで求まるので、これを事前に求めておいて、$g(i)$が$x$より小さくなったら枝刈りしてよい。これで満点が取れた。
でも、計算量がよくわからない。
2020年5月21日木曜日
ふか杯 5th contest E - すごろく
$f(i) :=$ マス$i$からゴールするまでにサイコロを振る回数の期待値、として降順にDPしたいが、振り出しに戻る場合の扱いを考えなくてはならない。
通常、ループを含む確率DPは左辺と右辺の両方に$f(i)$が登場する式が立式できて、$f(i) = ...$となるように整理すると遷移がわかるはずだが、この場合は紙の上で式変形するのは難しそうに見える。そこで、$f(1)$の係数も別にDPで求めることにする。つまり、$f(i) = a(i) + b(i)f(1)$と表して、$a, b$を降順で求める。
$x_i>0$なら
$$ a(i) = a(i + x_i) $$ $$ b(i) = b(i + x_i) $$$x_i = 0$なら
$$ a(i) = \frac{1}{6}(a(i+1) + ... + a(i+6)) + 1 $$ $$ b(i) = \frac{1}{6}(b(i+1) + ... + b(i+6)) $$$x_i = -1$なら
$$ a(i) = 0 $$ $$ b(i) = 1 $$これで$a(1), b(1)$が得られるので、答えは$f(1) = a(1)/(1-b(1))$と求まる。
2020年5月18日月曜日
第一回日本最強プログラマー学生選手権予選 C - Cell Inversion
区間の組み合わせの総数が求まれば、操作の順番の総数は$N!$を掛けて得られるので、前者を求めればよい。
$S$を左から走査して、閉じていない区間を保持しながらDPすることを考える。つまり、
$\operatorname{dp}[x][y] := x$文字目までみて、閉じていない区間が$y$個あるような場合の数
というDPをする。$x$文字目が$W$で$y$が偶数、もしくは$x$文字目が$B$で$y$が奇数なら、ここで$y$個の(閉じていない)区間のどれかを閉じるのが正しいので、
$$ \operatorname{dp}[x+1][y-1] \operatorname{+=} y \cdot \operatorname{dp}[x][y] $$$x$文字目が$B$で$y$が偶数、もしくは$x$文字目が$W$で$y$が奇数なら、さらに新しい区間を開始して反転を1増やすべきなので
$$ \operatorname{dp}[x+1][y+1] \operatorname{+=} \operatorname{dp}[x][y] $$このDPは${O}(N^2)$の形になっているが、実際にやってみると各$x$について有効な$y$は高々1つしかないことがわかるので、線形で書ける。
コンテスト当時にはまったくわからなくて、解説を読んでも天才解法に見えた問題だった。今見ると、いわゆる箱根駅伝DPを書けばアドホックな考察をしなくても解けてしまうことがわかる。
ただ、${O}(N^2)$のDPが見えているときに、それの延長として想定解が導ける場合とかなり難しい場合があって、コンテスト中にそちらにどこまで頭を使うかは微妙なところとは思う。今出ても、ムーブ次第ではまりかねない気がする。
ABC 168 F - . (Single Dot)
縦線と横線で分割される$(N+1)(M+1)$個くらいの矩形について、隣接している矩形との連結性を調べながらBFSすればよい……のだが、なかなか通らなかった。
$C_i = C_j$のような場合の扱いが問題だった。そういうケースがありえることは承知していて、間に面積0の矩形があると考えて問題ないと思っていたのだが、$(3, 1) - (5, 1), (4, 1) - (6, 1)$のように縦線が重なっている場合($\Leftrightarrow A_i \le B_j \land A_j \le B_i$)に、前者の左にある矩形→中間の(面積0の)矩形→右の矩形、のように本来移動できないところを迂回して移動できてしまう可能性があることに気づいた。結局、前処理の時点でつながっている線分は1本につなげてしまうことで解決した。
2020年5月17日日曜日
Google Code Jam 2020でのSBCLのトラブル その2
GCJ Round 2に出たが、Round 1に引き続いてSBCL絡みのトラブルにあってしまった。
以下の(特に意味のない)コードをSBCL 1.3.8 ~ 1.4.5に打ち込むとコンパイルが終了しない。
(defun test (n graph)
(let ((vector (make-array n :initial-element 1)))
(setf (aref vector 0) 0)
(let ((value 1))
(dotimes (i n)
(dolist (v (list 1))
(setf (aref vector v) value)
(dolist (y (aref graph v))
(print y)))))))
1.3.7→1.3.8と、1.4.5→1.4.6の変化を眺めた感じでは、make-arrayの最適化に関連して低レベルの問題が起こっていそうで、(declare (fixnum n))や(declare (notinline make-array))を宣言すると問題が解消する。詳細はわかっていない。
Security Updateのvisibleをとりあえず通しておこうとして起きた現象で、この対処に時間を費やしてしまった。自分の準備にも問題があって、ローカルではバージョン1.4.14を使っていたので単純に問題の把握が遅れたというのがある。(GCJの環境は1.3.14だが、Windowsリリースはないし、CodeChefの1.3.13で問題が起きたことがないので気にしていなかった。) 本格的にWSL環境に移ることを考えたほうがよいのかもしれない。
しかし、こんな基本的なコードが落ちるのはさすがに驚く……
コンテスト後にはさすがに凹んだけれど、去年よりは確実に強くなっている。来年も頑張ろう。
2020年5月11日月曜日
CodeChef May Challenge 2020 - Not a Real World Problem
部分点について。$N \le 15$なら全探索でよい。$H = 2$なら縦2マスの符号の状態(4通り)を持ちながら左から右にDPすればよさそう。
一般の場合について。燃やす埋めるでできたら話が早いと思ってyosupoさんの記事を眺めると、できそうだ。異なる色に塗ると罰金がかかるタイプの問題であることがポイントか。
以下、yosupoさんのフレームワークに従って考える。粒子$i$を正に塗る、負に塗るという言い方を使う。また、粒子$i$の載っているマスに書かれている数を$h_i$とする。
- $h_i \ge 0$の場合: $i$を正に塗ると$p_ih_i$円得られる。負に塗ると$p_ih_i$円失う。→ 最初から$p_ih_i$円持っているとする。$i$を負に塗ると$2p_ih_i$円失う。
- $h_i < 0$の場合: $i$を正に塗ると$p_ih_i$円失う。負に塗ると$p_ih_i$円得られる。→ 最初から$p_ih_i$円持っているとする。$i$を正に塗ると$2p_ih_i$円失う。
- 粒子$i, j$が隣り合っているとき、$i$を正(負)に、$j$を正(負)に塗ると$p_ip_j$円得られる。$i$を正(負)に、$j$を負(正)に塗ると$p_ip_j$円失う。→ 最初から$p_ip_j$円持っているとする。$i$を正(負)に、$j$を負(正)に塗ると$2p_ip_j$円失う。
これをそのままグラフにして、最大フローを流せばよい。
ほとんどの$h_{y, x}$に意味がないのはなんだったんだろう…… 誤読を疑って何度も確認してしまった。
CodeChef May Challenge 2020 - Triple Sort
3つの数のシフト操作は2つの互換でできていて、つまり偶置換なので、与えられた置換が奇置換だとどうやっても$1, 2, ..., N$に戻すことはできない。
偶置換の場合について具体的な手順を与えるために、与えられた置換を巡回置換に分解して考える。長さ$k(\ge 3)$の巡回置換$(p_1 p_2 ... p_k)$があるとき、$p_1, p_2, p_3$に操作を適用すると先頭の2つが正しい場所に収まって長さ$k-2$の巡回置換$(p_3 ... p_k)$が残る。$k=3$の場合はこの操作ですべての数が正しい場所に戻るので、結局$k$が奇数ならこの操作を最後まで繰り返せることになる。いっぽう$k$が偶数の場合は、長さ$2$の巡回置換、つまり互換が残るので、これらの処理を考える。2組の互換$(p_1 p_2), (p_3 p_4)$がある時、操作$p_1, p_2, p_3$と$p_2, p_3, p_4$を順に適用することで、4つの数がすべて正しい位置に戻る。こうして2組ずつ処理していったとき、偶置換であれば最後に端(=1つの互換)が残ることもないので、けっきょく常に$1, 2, ..., N$に戻せることになる。また、操作1回につき2つの数を正しい位置に戻せるので、操作回数の上限も満たせることがわかる。
CodeChef May Challenge 2020 - Sorting Vases
$M=0$なら巡回置換に分解して数える典型問題。また、$N=5$程度なら各順列を頂点として0-1BFSで探索すればよい。
満点について。まず、2つのロボットが与えられたときに、「少なくともいっぽうのインデックスが等しい」という関係が同値関係になっていることに注目する。このため、$N$個のインデックスはノーコストで自由に行き来できるまとまりに分割できる。
具体例を挙げて考える:
1
9 5
5 8 2 4 6 7 9 3 1
2 5
5 6
3 4
7 8
8 9
この入力をグラフで図示すると次のような感じになる:

各頂点は、コスト0で相互に行き来できるインデックスを1つにまとめたものである。また、辺$A \rightarrow B$は$A$に含まれる場所から$B$に含まれる場所にちょうど1つの数を移動させなければならないことを表す。たとえば$5$は最初インデックス$1$にあって、インデックス$5$に移動させたいので、頂点$1$から頂点$5(, 2, 6)$に辺を張っている。
こうしてグラフにしてみると、$M=0$の場合と考え方はあまり変わらないことに気づく。つまり、このグラフ上の長さ$k$の閉路は$k-1$回のスワップで解消できるので、グラフをいくつかの(辺素な)閉路に分割する問題であることがわかる。また、必要なスワップの回数は閉路の総数のみによって決まることも変わらない。
さて、閉路の総数だが、下のグラフのように分割方法によって異なる場合がある。
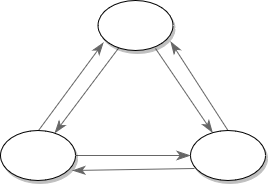
このグラフでは、長さ2の閉路を3つ選ぶことも長さ3の閉路を2つ選ぶこともできる。したがって、スワップの回数を減らすために、できるだけ多くの閉路に分割する方法を考えなければならない。ここまで考察を進めるとbitDPの形が見えた:
$\operatorname{dp}[S][x][y] :=$ 辺の集合$S$を使用済みで、いま作りかけている閉路(まだ閉じていない)の始点が$x$、終点が$y$である時の、今までに作った閉路の総数の最大値。
遷移が${O}(N)$なので計算量は${O}(N^32^N)$になる。オーダー的には微妙なところだが、大半の状態は無効だし、各$N$がすべて$18$ということもありえないので大丈夫だろう。割と余裕で通った。(計算量の評価がtightじゃないかも) 辺数が${O}(N)$だから隣接リストで持てば${O}(N^2 2^N)$だった。
CodeChef May Challenge 2020 - Chef and Rainbow Road
要約: $a_1, ..., a_N$から (1) 重複を許して選んで (2) どれも少なくとも1個以上選んで (3) 合わせて$N+K-1$個になるように選んで、積を取るとする。それらの総和を求めよ。
最低$1$個以上という条件を外して$K-1$個選ぶことにして、求まった値に$a_1...a_N$を掛ければよい。
多項式で考えるんだろうなという検討はつくが、ほとんど何も知らないのでmaspyさんの記事などを見て式を考える。とりあえず
$(1+a_1x+a_1^2x^2 + ...)(1+a_2x+a_2^2x^2 + ...) ... (1+a_Nx+a_N^2x^2 + ...)$
の第$K-1$項(0-based)を見ればよいことがわかる。この式は$((1-a_1x)(1-a_2x)...(1-a_Nx))^{-1}$と表せて、$(1-a_1x)(1-a_2x)...(1-a_Nx)$は分割統治してFFTすればよく、逆元もFFTで求まるらしいので、$K \le 10^5$の部分点1, 2はそれで取れる。
部分点3からはこの方針では無理そう。ところで、この間のlong challengeのまったく歯が立たなかった問題についてNyaanさんが記事を書いていたのを思い出して見に行ったら、部分分数分解というワードが出てきて使えそうと思う。
$$ \frac{1}{(1-a_1x)(1-a_2x)} = \frac{a_1}{(a_1-a_2)(1-a_1x)} + \frac{a_2}{(a_2-a_1)(1-a_2x)} $$と分解できるので、全部掛けると$1/(1-a_1 x)$の係数は$a_1^{N-1}/\prod_{j \neq 1} (a_1 - a_j)$になる。対称性により$1/(1-a_i x)$の係数は$a_i^{N-1}/\prod_{j \neq i} (a_i - a_j)$であり、これが$1+a_i x + a_i^2 x^2 + ...$に掛かっているので$x^{K-1}$の係数は$a_i^{K+N-2}/\prod_{j \neq i} (a_i - a_j)$とわかる。この値をすべての$i$について加算すれば答えが得られる。部分点3が取れた。
満点について。$a_i^{K+N-2}/\prod_{j \neq i} (a_i - a_j)$の分母の形を見るとヴァンデルモンド行列式やラグランジュ補間などが思い浮かぶので、ラグランジュ補間の解説を読んでいて$(x-a_1)...(x-a_N)$を微分したものに代入すればいいと気づく。多項式の値を$N$個の点について求める必要があるが、ググると${O}(N\log^2 N)$でできるらしい → 間に合った。
最終日に満点に気づいた。時間がなさすぎたのでbeetさんのライブラリを大急ぎで写経…… 長期コンテストでも終了直前に方針が立つと結局時間に追われることになるな。
CodeChef May Challenge 2020 - Binary Land
$1$が書いてあるマスから$1$が書いてあるマスへのパスの求め方だけ検討すればよい。
2地点間のパスの総数自体は単純なDPで求まる。DPの遷移は$N \times N$の行列で書けるので、行列積をセグメント木などに乗せれば${O}(N^3Q\log Q)$で解ける。また、クエリが単調なことを利用するとSWAGが使えて${O}(N^3Q)$になる。
満点を取るためにはもう少し頑張る必要がある。まず、遷移の行列が三重対角行列になっていることに注目すると、行列積は${O}(N^2)$になる。したがって、SWAGへのpushとpopはこの計算量でできる……が、三重対角行列同士の積が三重対角行列になるわけではないので、SWAGをfoldする時の掛け算はどうしても${O}(N^3)$になってしまう。しかし、pathクエリに対して必要なのは行列そのものではなく一点の値なので、そこだけ求めるのは${O}(N)$で可能だった。これで${O}(N^2Q)$になった。
これでもなかなかACできなかった。行列をなるべく陽に持たずに省略できる部分は省略して、定数倍高速化を徹底するとようやく通った。
CodeChef May Challenge 2020 - Buying a New String
たくさん解かれているのに部分点すらわからないので、書いたことのない文字列アルゴリズムだろうなと検討をつける。Aho-Corasickがいちばんそれっぽいので、貼るととりあえず部分点が取れた。
$|A||B|$個の文字列間で遷移の共通部分が多いことを利用できれば満点が取れそう。そして、そのためにはAho-Corasickをちゃんと理解する必要がありそう。しかし、ei1333さんのコードを見ていても理屈がよくわからないので、明らかな性質だけでなんとかすることにした:
- Aho-Corasickのマッチは部分文字列の一致をひとつずつカウントする。つまり、まとめてカウントしたりはできないので、素朴にやるとマッチする文字列の長さに対して${O}(N^2)$になる。とりあえず、トライ木を作ったらノード毎に重みの和をまとめておいたほうがよさそう。たぶんそれでオーダーも落ちる。
- Aho-Corasickの状態は今いるノードだけで決まる。つまり、ノードが同じで以降の文字列が同じならその後の遷移はすべて同じ。
以上に基づくと、次の配列を作っておけばよいはず:
$\operatorname{cumul}_A[i] := A$の区間$[0, i)$を走査した後のスコア
$\operatorname{node}_A[i] := A$の区間$[0, i)$を走査した後のノード
$\operatorname{cumul}_B[i] := B$の区間$[0, i)$を走査した後のスコアを$0$として、そこから最後まで走査して得られるスコア。
$\operatorname{node}_B[i] := B$の区間$[0, i)$を走査した後のノード
$A, B$をそれぞれ$[0, i_1,), [i_2, \operatorname{length}(B))$で切った時のスコアは$\operatorname{cumul}_A[i_1]$に$\operatorname{node}_A[i_1]$から$B[i2, \operatorname{length}(B))$を走査して得られるスコアを足したものになるが、この途中で、$B$の位置$i$を走査する際にノードが$\operatorname{node}_B[i]$と一致していることが確認できたら$\operatorname{cumul}_B[i]$を足して打ち切ってよい。単語の長さが高々26なので、$i_1$からそれだけ遷移すれば一致するはず。計算量はたぶんアルファベットの数を$\alpha$として${O}(\alpha|A||B| + \sum_i S_i)$。
そしてまだAho-Corasickを理解していない……
2020年5月2日土曜日
第二回 アルゴリズム実技検定
リアルタイム受験した。4時間40分かけて全完。前回に比べるとかなり苦戦した。
F
別解っぽいの:
$B_i$の降順に埋められるできるだけ早い日を埋めていく貪欲が成立する。(交換しても損しないことに注目すればよい。) このとき、$\operatorname{next}[i] :=$ $i$日目以降(inclusive)でまだ埋めていない最も早い日、として空きを管理する。$\operatorname{next}$を辿る際にpath compressionするとたぶん${O}(N\log N)$。
K
(を見るとネストの深さが+1され、)を見ると深さが-1されると考えると、文字を削除(=無視)するのは深さを変えないで次に進むことと解釈できる。したがって、次のようなDPが可能である:
$\operatorname{dp}[x][y] :=$ $1, ..., x$文字目まで見て、深さが$y$の場合の最小コスト
答えは$\operatorname{dp}[N][0]$に等しい。${O}(N^2)$。
L
$K$個の要素を選ぶ際、先頭から$x$番目(0-based)の数の元のインデックス$i$(0-based)は$i < N-D(K-x-1)$を満たす必要があり、その中で最小(タイブレークはもっとも左)の数を選べばよい。優先度付きキューでできる。
M
今回いちばん大変だった問題で、最後にACした。
数列$(C_i)$をいくつかつなげたものを走査して、各食事$x$についての情報を累積していく。具体的には、$\operatorname{table}[x]$に(日付, この日付までに食べた料理$x$の数, この日付までに食べた$x$以外の料理の数)の日付に関する昇順配列を作って、料理$x$が出るたびに情報を追加していった。こうすると、ある日付から一巡したときに食べる好みの料理の数と好みでない料理の数は二分探索でわかるので、何周するか計算すればよい。ただし、端の処理をするのがかなりつらかった……
N
平面走査する。$x$座標を圧縮しておいて$y$座標に関して走査した。
O
問題の条件を無視して最小全域木$T$を得たとする。$T$に$T$外の任意の辺$e := (u, v)$を追加すると閉路ができるが、この閉路上でもっとも重みの大きな($e$以外の)辺を除けば求める最小全域木$T_e$が得られる。(正当性は最適性条件により明らか……と言いたいところだが、そんなに簡単な証明を思いつかなかった。下に書いた。)この「辺の重みの最大値」は$T$上のパス$u - v$に関する$\max$クエリを処理すれば得られる。
やることはわかったのだが、そもそも木上のパスクエリを処理した経験があまりない。単純なオイラーツアーではmin/maxの処理ができないように見えるし、HL分解やLC木は持っていないし、Mo's algorithmでは${O}(1)$の遷移が思いつかないし、しばらく困っていた。HL分解を調べて書こうと決めたところで、そもそも更新がないのでLCAのbinary liftingがそのままmin/maxクエリにも使えることに気づいた。やっぱり経験がないとこういうことがぱっとわからないな。
証明: $e$のコストを$w$とし、このコストを$0$に変えたグラフを$G_0$とする。また、$G_0$のMST $T_0$が与えられたとして、そのコストの総和を$W_0$とする。(path optimality conditionより)$T_0$は$e$を必ず含むので、$T_0$は$G$上でコスト$W_0 + w$の全域木になっている。$G$の$e$を含む全域木 $T'$でこれより総コストの低いものが存在すると仮定して、総コストを$W'(< W_0 + w)$とする。$T'$は$G_0$の全域木でもあり、コストの総和は$W'-w$だが、$W'-w < W_0 + w -w = W_0$なので、$T_0$がMSTであるという仮定に反する。したがって、求める全域木は$G_0$のMSTであることがわかった。
あとは、上の作り方でできた全域木$T_e$が$G_0$上でMSTであることを示せばよい。$T_e$外の任意の辺$e'$を追加すると閉路ができるが、この閉路に含まれる$e$以外の辺は($T$の$G$におけるpath optimality conditionより)$e'$以下の重みを持つし、$e$自身は重み$0$なので、やはり$e'$以下の重みを持つ。したがって、$T_e$は$G_0$上でpath optimality conditionを満たす。$\square$
後半は有名事実だと思うけど若干雑…… 書き直すかも