CS Academy - Necromancer

• 問題
• AC

複雑な設定だが、考えるべきは各投票者がどの候補者をトップ（一番目）にした可能性があるか、だけである。

与えられた投票者$A$について、$A$の投票した候補者の部分列が$q_1, q_2, ..., q_l$であるとわかっているとする。ネクロマンサーの投票操作を最小で済ませるためには、候補者$1$にとって最善のケースを考えるべきである。$q_1 = 1$なら$A$は候補者$1$をトップにしたと考えれば良いし、$q_1, q_2, ..., q_l$に候補者$1$が含まれていない場合もやはり候補者$1$をトップにしたと考えてよい。その他の場合、つまり部分列の中に$1$が含まれているが最初ではない場合、$A$は$1$以外の候補をトップにしたことになる。$l = K$ならそれは$q_1$だし、$l \neq K$なら$q_2, ..., q_l$以外のいずれかの候補である。

さて、$1$以外に投票したことがわかっている候補者については、投票先を$2, 3, ..., K$にばらけさせて、得票数の最大値ができるだけ小さくなるようにしたい。その最小値がわかれば、ネクロマンサーはそれを超えるように候補者$1$の得票を増やせばよい。これは二分探索とフローで実現できる。つまり、得票数の最大値がある値$D$以下にできるかどうかを最大フローで判定すればよい。

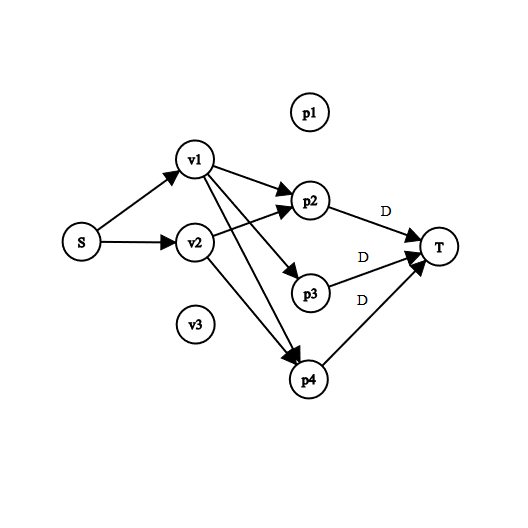
グラフの作り方としては、始点$S$を（投票先が1以外の）各投票者と容量$1$の辺でつなぎ、投票者をありえる投票先に容量$1$の辺でつなぎ、（1以外の）各候補者と終点$T$を容量$D$の辺でつなげばよい。

サンプルのケースでは次のようなグラフになる:

3人の投票者$v_1, v_2, v_3$について、4人の候補者$p_1, p_2, p_3, p_4$の中からありえる投票先につないでいる。何も書かれていない辺の容量は$1$である。候補者$1$は常に無視してよいし、投票者$3$も候補者$1$に投票しているとみなせるので無視してよいが、便宜上、図に書いている。
このグラフに流量$2$（$=S$から出ている辺の容量の合計）のフローが流せれば、得票数の最大値が$D$以下にできることがわかるので、二分探索で境界を探せば良い。