CodeChef - Unusual Queries

• 問題
• AC

山$i$の「次の山」は、$i<j$かつ$H_i < H_j$であるような最小の$j$である。(→ next greater element)　各山に向かって次の山から辺を張ったグラフは有向森であり、この森に$H_{N+1}=\infty$に対応する大頂点を加えると頂点$N+1$を根とする有向木(out-tree)になる。この木を$T$とする。この時、クエリは$T$の一部を切り取ったグラフの最も長いパスの頂点数を質問していることになる。

• クエリ$(L, R)$を処理する時、$r$を$R$より小さくしても得しないので、$r = R$を固定して$l \in [L, R]$について最大値が求まればよい。これは適当な列が得られていればRMQに帰着するはずだが、どうやってその列を得るかが問題となる。
• 任意の$R$について、$\operatorname{dp}_R$を$\operatorname{dp}_R[i] := l=i, r=R$の時の求める値、と定める。このとき、$\operatorname{dp}_{R+1}$は$\operatorname{dp}_R$上の$R+1$の部分木に含まれる各位置に+1したものになっている。
• $T$の頂点番号は$T$の帰りがけ順についているので、部分木への加算は$\operatorname{dp}_R$のある区間への加算になっている。

したがって、クエリ先読みができるなら$\operatorname{dp}_R$を区間max・区間addの遅延セグメント木で持って$R$の昇順に更新しつつ、各$R$に対応するクエリをまとめて処理すればよい。満点を取るにはオンラインで処理する必要があるが、これは永続化でできる。

この問題の場合はStarry Sky treeでいいので、普通の永続セグメント木と同じように素朴なpath copyingでできる。

---

わからなかった。上の方針はEditorialの方針とanubhavdharさんの書き込みのハイブリッドみたいなやつ。

小さい数を法とする二項係数

$\binom{n}{k} \mod M$を求めたいが、$M$が合成数だったり$k \ge M$だったりして階乗の逆元が得られない場合について。$n$が小さければパスカルの三角形を作ればよいが、$M$が小さい場合にも方法がある。https://discuss.codechef.com/t/your-approach-to-solve-sandwich/14618/13 より。

$M$をいくつかの互いに素な因数に分解してそれぞれを法として二項係数を求めれば、CRTで$\mod M$の値が得られる。したがって、次の問題が解ければよい:

問題: 素数の累乗$p^e$が与えられた時に$\binom{n}{k} \mod p^e$を求めよ。

$f(x, p) :=$ 階乗$x!$を非負整数$e, q$を使って$x! = p^e q$と表す時の最大の$q$

とする。言い換えると、$f(x, p)$は$x!$を$p$で割れる限り割ったものである。$n! = p^{e_1}f(n, p), k! = p^{e_2}f(k, p), (n-k)! = p^{e_3}f(n-k, p)$とするとき、二項係数$\binom{n}{k}$は次のように書ける:

$$ \binom{n}{k} = \frac{p^{e_1-e_2-e_3}f(n, p)}{f(k, p)f(n-k, p)} $$

$f(k, p), f(n-k, p)$は$p^e$と互いに素なので$\mod p^e$で逆元を持つ。したがって、$e_1, e_2, e_3$と$f(n, p), f(k, p), f(n-k, p)$が求まれば二項係数を計算できる。

前者、つまり$e_1, e_2, e_3$を求めるほうは簡単で、一般に階乗$x!$が$p$で割れる回数は$\sum_{i=1}^\infty \lfloor x/p^i \rfloor$に等しく（ルジャンドルの公式）、この式で素朴に計算すれば${O}(\log x)$で求まる。

次に$\mod p^e$で$f(x, p)$を計算する問題を考える。$f(x, p)$は$x!$から素因数$p$を除いたものなので、ひとまず階乗から$p$の倍数だけ分離して考えてみる: $X$を$1, 2, ..., x$のうちの$p$の倍数でない数の総積とするとき、$f(x, p) =Xf(\lfloor x/p \rfloor, p)$が成り立ち、${O}(\log x)$回の再帰で$f(0, p)=1$に帰着して$f(x, p)$が求まる。 （実際にはループでよい。）

あとは$X$を$\mod p^e$で求める方法が問題になるが、$p$の倍数の位置は$\mod p^e$で周期的なことを利用できる。最初に「$p$の倍数だけ飛ばした階乗$\mod p^e$」の長さ$p^e$のテーブルを作っておけば、$X$は繰り返し二乗法で${O}(\log x)$で計算できる。

全体の計算量は

• build: ${O}(p^e)$
• query: ${O}((\log n)^2)$

と評価できる。また、冒頭の任意の$M$を法とした二項係数を求める問題に関しては、

• build: ${O}(M)$
• query: ${O}((\log n )^2 \log \log M)$

となる。（$\log \log M$は$M$の異なる素因数の個数の評価。）

---

Lucasの定理の素数の累乗に関する拡張を使う方法もあるらしい。たぶんこちらのほうが速い。 https://arxiv.org/pdf/1301.0252.pdf

ARC 065 E - へんなコンパス

• 問題
• AC

点$a, b$の距離を$D$とする。全体を45度回転してチェビシェフ距離の問題に読み替えると、1つの点$(x, y)$から距離$D$にある点は$x \pm D , y\pm D$で定まる正方形の辺上にある。したがって、

• $v[t] := x$座標を$t$とする点を$y$座標の昇順に並べた列
• $h[t] := y$座標を$t$とする点を$x$座標の昇順に並べた列

を持っておけば、$(x, y)$から距離$D$にある点の数は4つの列$v[x \pm D], h[y \pm D]$の二分探索で数えられる。

ただ、問題が要求しているのは、単にマンハッタン距離が$D$であるような点のペアを数えることではなく、そのような点を結ぶ無向辺があるようなグラフを考えた時、辺$\{a, b\}$を含む連結成分について同じ量を数えることである。

ただ、この設定でもBFSをしながら同じことをやればよいように見える。つまり、$a$を始点にして、上記の数え上げをしながら距離$D$にある点をキューに入れていけばよい……が、これを素朴にやると$\Omega (N^2)$になってしまう。$o(N^2)$で数えるには、一度見た頂点を再び走査しないようにするために、その都度消していく必要がある。

そこで、$h(t), v(t)$をそれぞれ昇順の配列$h_s(t), v_s(t)$と平衡二分木$h_b(t), v_b(t)$の二通りで持つことにする。キューから点$(x, y)$を初めて取り出した時、次の処理をする:

• 点$(x, y)$をすべての平衡二分木から消去する。
• $v_b[x - D], v_b[x+D], h_b[y - D], h_b[y+D]$からそれぞれ区間$[y-D, y+D], [y-D, y+D], [x-D, x+D], [x-D, x+D]$に対応する4列をsplitして取り出す。$v_b[x - D], v_b[x+D], h_b[y - D], h_b[y+D]$には残った左右の区間をmergeして入れておく。
• 4つの列上の頂点をすべてキューに入れ、$v_b, h_b$からすべて除く。
• $(x, y)$と4つの列上の点によるペアを数える。
  • 配列$v_s[x-D]$の$[y-D, y+D]$に対応する区間の長さを結果に加算する。
  • 配列$v_s[x+D]$の$[y-D, y+D]$に対応する区間の長さを結果に加算する。
  • 配列$v_s[y-D]$の$[x-D, x+D]$に対応する区間の長さを結果に加算する。
  • 配列$v_s[y+D]$の$[x-D, x+D]$に対応する区間の長さを結果に加算する。
  • 正方形の4頂点$(x \pm D, y \pm D)$に穴が存在する場合は2回数えているので、重複を引く。

すべてのペアを2回ずつ数えているので、最後に2で割ることに注意。

AHC 001 A - Atcoder Ad

• 問題
• 最終提出

49,567,989,183で暫定17位だった。→システス後18位だった。

焼きなましをした。遷移は上のように隣の広告に割り込むような操作とそのバリエーションを中心にしたが、広告の単純な伸縮も残した。温度はかなり高めに設定していて伸縮のほうはほぼ通るので、単に状態の多様性を生むだけの遷移になっていたと思う。

以下は効果が大きかったもの:

• しばらく最大スコアが更新されなかったら、スコアの低い広告周辺を上の操作で無理やり変形するようなキックを入れた。
• 近い広告は基本的にはくっついていたほうが遷移がしやすいので、得点計算の式を希望より大きいぶんにはかまわない($p_i = 1- (1- \min(1, s_i/r_i))^2$)というものにして、最後に縮めることにした。

---

以下、ほかの人の解法等を眺めての感想。

• うまくいっていない部分が（スコアの低い広告という形で）特定しやすいし、その周辺をなんとかすれば問題ないだろうという想像でキックの調整を頑張っていたが、多点スタートをもう少しちゃんと考えるべきだったかも。
• キックで$1\times1$に縮める、はなるほどと思った。自分の複雑な操作よりよほど単純で効果的に見える。
• 最後まで配布ツールによるもの以外のビジュアライズを一切せずに結果を見て良くない部分を直すような操作を考えていたが、動画などで見てわかることも多そうだと思った。次は準備したい。
• それっぽい変形を書いては調整を頑張るだけに時間を費やしていて、問題の性質について真剣に考えている時間が短かったな。（試すことリストを消化するだけで時間が過ぎていって、スコアもまあまあ伸びたので考えるタイミングがなかったというのはある。）順位がよかったのはたまたまだろうなと思った。

JOI2021 本選 C - 集合写真

• 問題
• AC

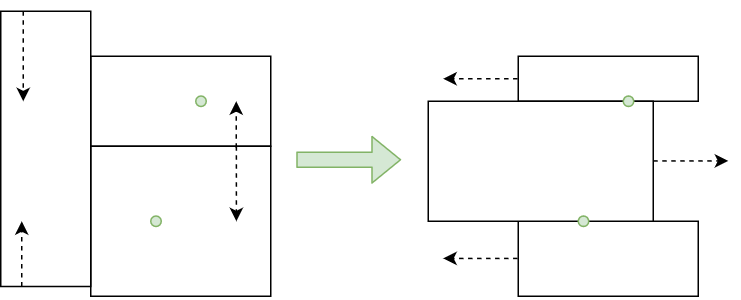
以下、すべて0-basedに直して考えている。

最終形は$2 1 0 |4 3|8 7 6 5$のように、$0, 1, ..., N-1$をいくつかの連続部分列に区切って各区間を反転させたものになっている。

$\operatorname{dp}[x] =$ 先頭から$x$個の階段に$0, 1, ..., x-1$を有効な順番で並べる場合の最小交換数

としてDPができそう。

DPの遷移を考える。位置$0, 1, ..., x-1$に人$0, 1, ..., x-1$を配置済みとして、位置$x$から$x, x+1, ..., y-1$を逆順に並べる場合のコストを$f[x][y]$とすると、$\operatorname{dp}[y] \leftarrow \max(\operatorname{dp[y]}, \operatorname{dp}[x] + f[x][y])$のように配るDPが${O}(N^2)$でできる。

次に$f$の求め方を考える。与えられた列の中に散らばっている数$x, x+1, ..., y-1$を位置$x, x+1, ..., y-1$に逆順で整列させる時、$c[i][j] :=$ 数$i$の左にある$j$以上の数の総数として、だいたい$c[x][x] + c[x+1][x] + ... + c[y-1][x]$回の交換をして$x, x+1, ..., y-1$を前のほうに持ってくることになるが、この際、与えられた列上での$x, x+1, ..., y-1$の順番を考えた時に、既に転倒が起きているぶんの交換はしなくてよい。そこで、$\operatorname{inv}[x][y] :=$ 与えられた列から$x, x+1, ..., y-1$を抜き出した部分列の転倒数、とすると

$$ f[x][y] = c[x][x] + ... + c[y-1][x] - \operatorname{inv}[x][y] $$

と求まる。$c$は累積和と同じように構成できて、さらにその累積和$C[x][y] := c[0][y] + ... + c[x-1][y]$を取っておけば

$$ f[x][y] = C[y][x] - C[x][x] - \operatorname{inv}[x][y] $$

と求まる。

最後に$\operatorname{inv}$の作り方を考える。ここでは$\operatorname{inv}[x][y-1]$と$\operatorname{inv}[x][y]$の差分、つまり、与えられた列上の$x, x+1, ..., y-2$に対応する部分列に（与えられた順番通りに）$y-1$を挿入した時の転倒数の増分を考える。この増分は与えられた列上で$y-1$の後ろにあって$[x, y-1)$に含まれる数の総数に等しい。$y-1$の後ろよりも前にある数のほうが（$c$を使って）表しやすいので、さらにこれを$(y-1-x) -$($y-1$の前にあって$[x, y-1)$に含まれる数の総数)と言い換える。この増分は上で求めた$c$を使って表せて、結局

$$ \operatorname{inv}[x][y] \leftarrow \operatorname{inv}[x][y-1] + (y-1-x) - (c[y-1][x] - c[y-1][y]) $$

と遷移できる。

これで、全体として${O}(N^2)$で計算できたことになる。